Giáo án Toán Lớp 10 (Cánh diều) - Bài tập cuối chương VI

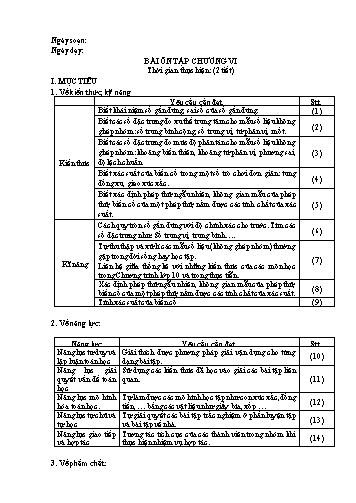
Ngày soạn:
Ngày dạy:
BÀI ÔN TẬP CHƯƠNG VI
Thời gian thực hiện: (2 tiết)
I. MỤC TIÊU
1. Về kiến thức, kỹ năng
Yêu cầu cần đạt
Stt
Kiến thức
Biết khái niệm số gần đúng, sai số của số gần đúng.
(1)
Biết các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm: số trung bình cộng, số trung vị, tứ phân vị, mốt.
(2)
Biết các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm: khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn. 
(3)
Biết xác suất của biến cố trong một số trò chơi đơn giản: tung đồng xu, gieo xúc xắc.
(4)
Biết xác định phép thử ngẫu nhiên, không gian mẫu của phép thử, biến cố của một phép thử, nắm được các tính chất của xác suất.
(5)
Kĩ năng
Cách quy tròn số gần đúng với độ chính xác cho trước. Tìm các số đặc trưng như: Số trung vị, trung bình.
(6)
Tự thu thập và xử lí các mẫu số liệu (không ghép nhóm) thường gặp trong đời sống hay học tập.
Liên hệ giữa thống kê với những kiến thức của các môn học trong Chương trình lớp 10 và trong thực tiễn.
(7)
Xác định phép thử ngẫu nhiên, không gian mẫu của phép thử, biến cố của một phép thử, nắm được các tính chất của xác suất.
(8)
Tính xác suất của biến cố
(9)
2. Về năng lực: 
Năng lực
Yêu cầu cần đạt
Stt
Năng lực tư duy và lập luận toán học
Giải thích được phương pháp giải vận dụng cho từng dạng bài tập.
(10)
Năng lực giải quyết vấn đề toán học
Sử dụng các kiến thức đã học vào giải các bài tập liên quan.
(11)
Năng lực mô hình hóa toán học.
Tự làm được các mô hình học tập như con xúc xắc, đồng tiền,  bằng các vật liệu như giấy bìa, xốp 
(12)
Năng lực tự chủ và tự học
Tự giải quyết các bài tập trắc nghiệm ở phần luyện tập và bài tập về nhà.
(13)
Năng lực giao tiếp và hợp tác
Tương tác tích cực của các thành viên trong nhóm khi thực hiện nhiệm vụ hợp tác.
(14)
3. Về phẩm chất: 
Phẩm chất
Yêu cầu cần đạt
STT
Trách nhiệm
Có ý thức hỗ trợ, hợp tác với các thành viên trong nhóm để hoàn thành nhiệm vụ.
(15)
Chăm chỉ
Tích cực phát biểu, xây dựng bài và tham gia các hoạt động nhóm
(16)
Nhân ái
Có ý thức tôn trọng ý kiến của các thành viên trong nhóm khi hợp tác
(17)
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: Tivi, laptop, giấy A0, bút lông, phiếu học tập, phấn màu,.
III. TIẾN TRÌNH DẠY HỌC:
Hoạt động
Mục tiêu
Nội dung
PPDH, KTDH
Sản phẩm
Công cụ đánh giá
Hoạt động 1: Thống kê
Hoạt động 1.1: Khởi động
1, 3, 6, 10, 13, 15, 16, 17
Các kiến thức đã học trong ba bài đầu của chương VI
- Phương pháp: giải quyết vấn đề, hợp tác
- Kĩ thuật giao nhiệm vụ, chia nhóm
Phiếu trả lời của cá nhân học sinh
Câu hỏi và đáp án
Hoạt động 1.2: 
Bứt phá
2, 3, 7, 10, 11, 15, 16, 17
Bài tập tự luận về các số đặc trưng đo xu thế trung tâm và các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm.
- Phương pháp: khám phá, giải quyết vấn đề, hợp tác.
- Kĩ thuật: chia nhóm, 321
Bảng báo cáo của học sinh các nhóm
Câu hỏi chuẩn đoán
Hoạt động 1.3: 
Về đích
2, 3, 7, 10, 11, 15, 16, 17
Tự thu thập và xử lí các mẫu số liệu (không ghép nhóm) thường gặp trong đời sống hay học tập
- Phương pháp: trực quan, giải quyết vấn đề
- Kĩ thuật: chia nhóm, 321
- Câu trả lời của học sinh.
- Bảng trả lời của các nhóm
Câu hỏi và đáp án
Hoạt động 2: Xác suất
Hoạt động 2.1: Luyện tập
4, 5, 8, 9, 10, 11, 12, 14, 15, 16, 17 
Xác định phép thử ngẫu nhiên, không gian mẫu của phép thử, biến cố của một phép thử, nắm được các tính chất của xác suất. Tính xác suất của biến cố.
- Phương pháp: giải quyết vấn đề.
- Kĩ thuật: chia nhóm
Bảng ghi chép phần trả lời câu hỏi của học sinh
Câu hỏi và đáp án 
Hoạt động 2.2: Vận dụng
5, 9, 10, 13, 14, 15, 16, 17
Xác suất của biến cố để giải bài toán về thực tế.
- Phương pháp: giải quyết vấn đề.
- Kĩ thuật: chia nhóm
Bảng ghi chép phần trả lời câu hỏi của học sinh
Câu hỏi và đáp án 
Hoạt động 1: Thống kê
Hoạt động 1.1: Khởi động (9p)
a) Mục tiêu:
	- Tạo hứng thú cho HS. 
	- HS nhớ lại các kiến thức đã học trong ba bài đầu của chương VI
b) Nội dung: HS trả lời 5 câu hỏi TNKQ theo nhóm nhỏ
Câu 1. Thống kê số học sinh đang tham gia học tập ở trường THPT trên địa bạn huyện năm 2022 là:
Tuổi
16
17
18
19
Tần số
9
11
7
3
N = 30
 Tần suất của giá trị x = 18 là đã cho là
 A. 60%.	B. 23,33%.	C. 36,66%.	D. 36,67%. 
Câu 2. Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A như sau:
	 Số trung vị của bảng số liệu trên là
 A. .	B. .	C. .	D. . 
Câu 3. Thống kê size áo bán ra trong tháng 2 năm 2022 của một cửa hàng chuyên bán quần áo cho trẻ em nhỡ như sau: 
Size
9
10
11
12
13
14
15
16
17
18
19
Tần số
1
1
3
5
8
13
19
24
14
10
2
N=100
 Tính độ lệch chuẩn?
 A.1,96.	 B. 1,97 	C. 1,99 	D.3,96
Câu 4. Thống kê bậc lương của 45 viên chức của một cơ quan nhà nước trong năm 2022 là:
Bậc lương
1
2
3
4
5
6
7
Số người
2
3
7
15
10
6
2
N = 45
 Tính bậc lương trung bình ?
 A.4	 B. 4,2 	C. 4,4 	D. 4,5
Câu 5. Lớp 10A có 40 học sinh. Tỉ số phần trăm về phương tiện mà các bạn đến trường được mô tả như biểu đồ ở Hình 7. Có bao nhiêu bạn đi xe đạp đến trường?
 A.16 B. 4 	C. 12 	D. 8
c) Sản phẩm: 1B – 2D – 3C – 4B – 5A
d) Tổ chức thực hiện:
Bước 1: Giao nhiệm vụ: 
 - Giáo viên yêu cầu HS tham gia tiết học theo Tổ dưới hình thức một trò chơi gồm 3 hoạt động: Tổ 1, Tổ 2, Tổ 3, Tổ 4. Mỗi tổ chia thành 3 nhóm nhỏ theo bàn.
 - Giáo viên phổ biến cách chơi của hoạt động 1: Giáo viên lần lượt chiếu 5 câu hỏi, Mỗi câu hỏi có thời gian suy nghĩ là 1 phút. Sau 1 phút các nhóm nhỏ đồng thời giơ đáp án trả lời theo hiệu lệnh của GV. Mỗi nhóm có câu trả lời đúng thì Tổ được cộng thêm 2 điểm. Phân công thư kí.
Bước 2: Thực hiện nhiệm vụ: 
- Các nhóm nhỏ thảo luận và chuẩn bị giơ đáp án
Bước 3: Báo cáo, thảo luận: 
 - Các nhóm nhỏ giơ đáp án theo hiệu lệnh của GV
Bước 4: Kết luận, nhận định: 
- GV gọi đại diện 1, 2 nhóm nhỏ giải thích. Gọi đại diện các nhóm nhỏ còn lại nhận xét. 
- GV nhận xét, công bố kết quả đúng.
- Hết 5 câu hỏi GV yêu cầu thư kí tổng kết điểm của các Tổ (Điểm tối đa của mỗi tổ sau hoạt động 1 là 30 điểm)
Hoạt động 1.2: Bứt phá (14p)
a) Mục tiêu:
- HS rèn kĩ năng giải bài tập tự luận về các số đặc trưng đo xu thế trung tâm và các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm.
b) Nội dung: HS thảo luận theo Tổ và trình bày bài tự luận trên giấy A0 (hoặc bảng phụ, hoặc giấy A4 – GV chiếu bài của HS lên tivi thông qua điện thoại)
Bài tập: Có 982.728 thí sinh tham gia thi bài thi Toán trong kì thi THPT năm 2022 với phổ điểm thi như sau:
Dựa vào phổ điểm thi hãy xác định:
Số học sinh đạt điểm tối đa (5 điểm)
Số học sinh bị điểm liệt (5 điểm)
Điểm số có nhiều thí sinh đạt nhất (5 điểm)
Số học sinh đạt điểm giỏi (5 điểm)
*Điểm trung bình (10 điểm)
c) Sản phẩm: Bài làm của HS trên giấy A0 (hoặc bảng phụ, hoặc bảng phụ, hoặc giấy A4 – GV chiếu bài của HS lên tivi thông qua điện thoại)
Số học sinh đạt điểm 10 là 35
Số học sinh bị điểm liệt là 4 + 1 + 3 + 6 + 42 + 109 = 165
Điểm số có nhiều thí sinh đạt nhất là 7.8 
Số học sinh đạt điểm giỏi là 214717 chiếm 21,85%
Điểm trung bình 6,47
d) Tổ chức thực hiện:
Bước 1: Giao nhiệm vụ: 
 - Giáo viên cho bài, biểu điểm, thời gian thực hiện nhiệm vụ là 10 phút.
 - Câu e. học sinh có thể sử dụng quyền trợ giúp từ giáo viên. Nếu sử dụng quyền trợ giúp từ giáo viên thì học sinh sẽ bị trừ 5 điểm cho câu e.
 - Trợ giúp: gợi ý “biết tổng số điểm của 982.728 thí sinh là 6.354.561,4 điểm”
Bước 2: Thực hiện nhiệm vụ: 
- HS thảo luận theo từng Tổ, trình bày bài vào giấy hoặc bảng phụ
Bước 3: Báo cáo, thảo luận: 
 - GV cử đại diện của 1 Tổ lên bảng giải thích lại cách làm, mời 3 Tổ còn lại đưa ra lời nhận xét về bài làm của các Tổ bạn và bài làm của Tổ mình theo Kĩ thuật 321.
Bước 4: Kết luận, nhận định: 
- GV nhận xét, cho điểm các Tổ. Trao đổi thêm một số thông tin về kì thi.
- Thư kí tổng kết điểm của các đội qua 2 hoạt động
Hoạt động 1.3: Về đích (20p)
a) Mục tiêu:
- HS rèn kĩ năng tự thu thập và xử lí các mẫu số liệu (không ghép nhóm) thường gặp trong đời sống hay học tập
b) Nội dung: HS tự thu thập và xử lí các mẫu số liệu (không ghép nhóm) thường gặp trong đời sống hay học tập theo Tổ
c) Sản phẩm: Báo cáo của HS trên giấy A0 hoặc trên word, excel, powerpoint
d) Tổ chức thực hiện:
Bước 1: Giao nhiệm vụ: 
 	- Ở tiết học trước giáo viên giao cho HS các Tổ tự thảo luận chọn chủ đề, thu thập và xử lí các mẫu số liệu (không ghép nhóm) thường gặp trong đời sống hay học tập và báo cáo:
 +) Bảng số liệu
 +) Bảng tần số, tần suất
 +) Tính các số trung bình cộng, số trung vị, tứ phân vị, khoảng biến thiên, khoảng tứ phân vị, mốt, phương sai, độ lệch chuẩn của bảng số liệu. 
 +) Vẽ biểu đồ minh họa
 +) Đưa ra nhận xét 
(Thông thường HS sẽ chọn các chủ đề như Điểm kiểm tra thường xuyên của các thành viên trong tổ, Số người trong một gia đình của các thành viên trong tổ, Bảng chiều cao của các học sinh trong tổ )
 - Điểm cho phần báo cáo tối đa là 30 điểm, phần thuyết trình và phản biện tối đa là 10 điểm.
Bước 2: Thực hiện nhiệm vụ: 
	 - HS thảo luận theo từng Tổ chọn chủ đề, thu thập và xử lí các mẫu số liệu (không ghép nhóm) thường gặp trong đời sống hay học tập và làm báo cáo.
Bước 3: Báo cáo, thảo luận: 
 - GV cử đại diện của 4 Tổ lần lượt lên trình bày (mỗi Tổ có 3 phút trình bày), mời 3 Tổ còn lại đặt câu hỏi cho Tổ bạn trả lời.
Bước 4: Kết luận, nhận định: 
	- GV nhận xét, cho điểm các Tổ.
	- Thư kí tổng kết điểm của các đội qua 3 hoạt động, công bố Tổ thắng cuộc và trao phần thưởng. (Tổng điểm tối đa của cả ba hoạt động là 100 điểm).
Hoạt động 2: Xác suất
Hoạt động 2.1: Luyện tập (25 phút)
a) Mục tiêu: HS áp dụng tất cả các kiến thức về xác suất của biến cố.
b) Nội dung: 
Bài 1. Gieo một đồng tiền cân đối và đồng chất 3 lần.
 a) Xác định không gian mẫu
 b) Tính xác suất của các biến cố sau:
 A: "Lần đầu gieo được mặt sấp"
 B: "Có ít nhất một lần gieo được mặt sấp"
Bài 2. Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất ba lần. Tính xác suất mặt sáu chấm xuất hiện ít nhất một lần. 
Bài 5 (SGK). Trong một hội thảo quốc tế có 10 chuyên gia đến từ các nước ở châu Á, 12 chuyên gia đến từ các nước ở châu Âu. Chọn ngẫu nhiên 2 chuyên gia vào ban tổ chức. Xác suất để chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức là bao nhiêu?
Bài 6 (SGK). Trong một buổi khiêu vũ có đúng 10 cặp vợ chồng. Chọn ngẫu nhiên 2 người lên khiêu vũ đầu tiên. Xác suất để 2 người được chọn là vợ chồng là bao nhiêu?
Bài 7 (SGK). Một lô hàng có 20 sản phẩm bao gồm 16 chính phẩm và 4 phế phẩm. Chọn ngẫu nhiên 3 sản phẩm. 
Có bao nhiêu kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm?
Xác suất của biến cố” Cả 3 sản phẩm được chọn là chính phẩm” bằng bao nhiêu? 
Bài 8 (SGK). Trong một hộp có 20 chiếc thẻ được viết các số 1, 2, 3, ., 20 sao cho mỗi thẻ chỉ viết một số và hai thẻ khác nhau viết hai số khác nhau. Chọn ngẫu nhiên 2 chiếc thẻ. Tính xác suất của biến cố “hai thẻ được chọn có tích của hai số được viết trên đó là số lẻ”.
c) Sản phẩm:
Bài 1. Lời giải: 
Kí hiệu : S là đồng tiền ra mặt sấp và N là đồng tiền ra mặt ngửa
Không gian mẫu gồm 8 phần tử:
Ω = {SSS, SSN, NSS, SNS, NNS, NSN, SNN, NNN}
Số phần tử của không gian mẫu: 
A:"Lần đầu xuất hiện mặt sấp"
A ={SSS, SSN, SNS, SNN} 
Vậy 
B: " Có ít nhất một lần gieo được mặt sấp "
B = { SSS, SSN, SNS, SNN, NSS, NSN, NNS}
Bài 2. Lời giải: 
 Gọi biến cố : “Mặt sáu chấm xuất hiện ít nhất một lần”
 Ta có .
 Biến cố : “Mặt sáu chấm không xuất hiện lần nào”. Ta có .
 .
Bài 5 (SGK). Lời giải: 
Tổng số chuyên gia tham gia hội thảo là: 10+12=22 chuyên gia.
Chọn ngẫu nhiên 2 chuyên gia vào tổ chức, mỗi cách chọn là một tổ hợp chập 2 của 22 phần tử. Số phần tử của không gian mẫu là: 
Xét biến cố A: “Chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức”. Chọn 1 chuyên gia đến từ các nước châu Á có cách, chọn một chuyên gia đến từ các nước châu Âu có cách nên 
 Vậy xác suất để chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức là:
Bài 6 (SGK). Lời giải:
Tổng số người tham gia khiêu vũ là: 2.10=20 người
Chọn 2 người trong số 10 cặp vợ chồng để khiêu vũ, mỗi cách chọn là một tổ hợp chập 2 của 20 phần tử. Số phần tử của không gian mẫu là: 
Xét biến cố B: “2 người được chọn là vợ chồng”. Có 10 cặp vợ chồng nên 
Vậy xác suất để 2 người được chọn là vợ chồng là:
Bài 7 (SGK). Lời giải:
a) Một lô hàng có 20 sản phẩm bao gồm 16 chính phẩm và 4 phế phẩm. Chọn ngẫu nhiên 3 sản phẩm, mỗi cách chọn là một tổ hợp chập 3 của 20 sản phẩm. Số phần tử của không gian mẫu là: 
 b) Biến cố A: “Cả 3 sản phẩm được chọn là chính phẩm”. Lấy 3 chính phẩm từ 16 chính phẩm nên 
 Vậy xác suất của biến cố” Cả 3 sản phẩm được chọn là chính phẩm” bằng: 
Bài 8 (SGK). Lời giải:
 Trong một hộp có 20 chiếc thẻ được viết các số 1, 2, 3, ., 20 sao cho mỗi thẻ chỉ viết một số và hai thẻ khác nhau viết hai số khác nhau. Chọn ngẫu nhiên 2 chiếc thẻ từ 20 thẻ, Số phần tử của không gian mẫu là: 
 Từ 1 đến 20 có 10 số lẻ. Xét biến cố A: “Hai thẻ được chọn có tích của hai số được viết trên đó là số lẻ”. Để tích hai số được viết trên đó là số lẻ thì hai thẻ sẽ được lấy từ hai thẻ mà hai số viết trên đó là hai số lẻ nên 
Vậy xác suất của biến cố “hai thẻ được chọn có tích của hai số được viết trên đó là số lẻ” là: 
 Tổ chức thực hiện:
Bước 1: Giao nhiệm vụ.
 GV: Chia lớp thành 4 nhóm. Giao nhiệm vụ cho từng nhóm. Cho nhóm học sinh bốc chọn bài, bài 1, 2 không trong sách bốc lấy 1 bài, bài 5,6,7,8 trong SGK bốc lấy 1 bài. Mỗi nhóm làm 2 bài. 
 HS: Nhận nhiệm vụ.
Bước 2: Thực hiện nhiệm vụ
 GV: Điều hành, quan sát, hỗ trợ 
 HS: 4 nhóm tự phân công nhóm trưởng, hợp tác thảo luận thực hiện nhiệm vụ. Trình bày bài vào bảng phụ.
Bước 3 : Báo cáo, thảo luận
 Đại diện nhóm trình bày kết quả thảo luận
	Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ hơn các vấn đề
Bước 4: Kết luận, nhận định
 GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. 
Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo
Hoạt động 2.2: Vận dụng ( 20 phút)
a) Mục tiêu: HS áp dụng tất cả các kiến thức về xác suất của biến cố để giải bài toán về thực tế.
b) Nội dung: 
Câu 1: Một hộp có 5 viên bi đỏ, 3 viên bi vàng và 4 viên bi xanh. Chọn ngẫu nhiên từ hộp 4 viên bi, tính xác suất để 4 viên bi được chọn có số bi đỏ lớn hơn số bi vàng và nhất thiết phải có mặt bi xanh.
 A. 	 B. 	C. 	D. 
Câu 2: Có 3 bó hoa. Bó thứ nhất có 8 hoa hồng, bó thứ hai có 7 bông hoa ly, bó thứ ba có 6 bông hoa huệ. Chọn ngẫu nhiên 7 hoa từ ba bó hoa trên để cắm vào lọ hoa, tính xác suất để trong 7 hoa được chọn có số hoa hồng bằng số hoa ly.
 A. 	 B. 	C. 	D. 
Câu 3: Có học sinh của một trường THPT đạt danh hiệu học sinh xuất sắc trong đó khối có học sinh nam và học sinh nữ, khối có học sinh nam. Chọn ngẫu nhiên học sinh bất kỳ để trao thưởng, tính xác suất để học sinh được chọn có cả nam và nữ đồng thời có cả khối và khối .
 A. 	 B. 	 C. 	 D. 
Câu 4: Giải bóng chuyền VTV Cup gồm đội bóng tham dự, trong đó có đội nước ngoài và đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành bảng và mỗi bảng có đội. Tính xác suất để đội bóng của Việt Nam ở bảng khác nhau.
 A. 	 B. 	C. 	D. 
c) Sản phẩm:
Câu 1: Lời giải: 
Không gian mẫu là số cách chọn ngẫu nhiên 4 viên bi từ hộp chứa 12 viên bi. Suy ra số phần tử của không gian mẫu là .
Gọi là biến cố 4 viên bi được chọn có số bi đỏ lớn hơn số bi vàng và nhất thiết phải có mặt bi xanh. Ta có các trường hợp thuận lợi cho biến cố là:
 TH1: Chọn 1 bi đỏ và 3 bi xanh nên có cách.
 TH2: Chọn 2 bi đỏ và 2 bi xanh nên có cách.
 TH3: Chọn 3 bi đỏ và 1 bi xanh nên có cách.
 TH4: Chọn 2 bi đỏ, 1 bi vàng và 1 bi xanh nên có cách.
Suy ra số phần tử của biến cố là .
Vậy xác suất cần tính . Chọn C.
Câu 2: Lời giải: 
 Không gian mẫu là số cách chọn ngẫu nhiên 7 hoa từ ba bó hoa gồm 21 hoa.
 Suy ra số phần tử của không gian mẫu là .
 Gọi là biến cố 7 hoa được chọn có số hoa hồng bằng số hoa ly. Ta có các trường hợp thuận lợi cho biến cố là:
 TH1: Chọn 1 hoa hồng, 1 hoa ly và 5 hoa huệ nên có cách.
 TH2: Chọn 2 hoa hồng, 2 hoa ly và 3 hoa huệ nên có cách.
 TH3: Chọn 3 hoa hồng, 3 hoa ly và 1 hoa huệ nên có cách.
Suy ra số phần tử của biến cố là .
Vậy xác suất cần tính Chọn D.
Câu 3: Lời giải. Không gian mẫu là số cách chọn ngẫu nhiên 3 học sinh từ 13 học sinh.
 Suy ra số phần tử của không gian mẫu là .
 Gọi là biến cố học sinh được chọn có cả nam và nữ đồng thời có cả khối và khối . Ta có các trường hợp thuận lợi cho biến cố là:
TH1: Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có cách.
TH2: Chọn 1 học sinh khối 11; 2 học sinh nữ khối 12 có cách.
TH3: Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có cách.
Suy ra số phần tử của biến cố là .
Vậy xác suất cần tính Chọn A.
Câu 4: Lời giải: 
Không gian mẫu là số cách chia tùy ý đội thành bảng.
Suy ra số phần tử của không gian mẫu là .
Gọi là biến cố đội bóng của Việt Nam ở bảng khác nhau.
+ Bước 1. Xếp đội Việt Nam ở bảng khác nhau nên có cách.
+ Bước 2. Xếp đội còn lại vào bảng này có cách.
 Suy ra số phần tử của biến cố là .
Vậy xác suất cần tính . Chọn C.
 Tổ chức thực hiện:
Bước 1: Giao nhiệm vụ
GV: Chia lớp thành 4 nhóm. Mỗi nhóm bốc 1 bài và làm bài vừa bốc được.
HS: Nhận nhiệm vụ.
Bước 2: Thực hiện nhiệm vụ
GV: Điều hành, quan sát, hỗ trợ 
HS: 4 nhóm tự phân công nhóm trưởng, hợp tác thảo luận thực hiện nhiệm vụ. Trình bày bài vào bảng nhóm.
Bước 3 : Báo cáo, thảo luận
Đại diện nhóm trình bày kết quả thảo luận
Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ hơn các vấn đề
Bước 4: Kết luận, nhận định
- GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. 
- Chốt kiến thức tổng thể trong bài học.