Giáo án Toán Lớp 10 (Cánh diều) - Thực hành phần mềm GeoGebra

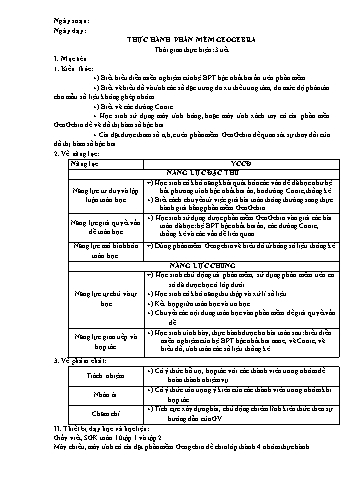
Ngày soạn:
Ngày dạy:
THỰC HÀNH PHẦN MỀM GEOGEBRA 
Thời gian thực hiện: 3 tiết
I. Mục tiêu
1. Kiến thức:
	+) Biết biểu diễn miền nghiệm của hệ BPT bậc nhất hai ẩn trên phần mềm
	+) Biết vẽ biểu đồ và tính các số đặc trưng đo xu thế trung tâm, đo mức độ phân tán cho mẫu số liệu không ghép nhóm
	+) Biết vẽ các đường Conic
	+ Học sinh sử dụng máy tính bảng, hoặc máy tính xách tay có cài phần mền GeoGebra để vẽ đồ thị hàm số bậc hai. 
	+ Cài đặt được tham số a,b,c trên phần mềm GeoGebra để quan sát sự thay đổi của đồ thị hàm số bậc hai
2. Về năng lực:
Năng lực
YCCĐ
NĂNG LỰC ĐẶC THÙ
Năng lực tư duy và lập luận toán học
+) Học sinh có khả năng khái quát hóa các vấn đề đã học như hệ bất phương trình bậc nhất hai ẩn, ba đường Conic, thống kê
+) Biết cách chuyển từ việc giải bài toán thông thường sang thực hành giải bằng phần mềm GeoGebra
Năng lực giải quyết vấn đề toán học
+) Học sinh sử dụng được phần mềm GeoGebra vào giải các bài toán đã học: hệ BPT bậc nhất hai ẩn, các đường Conic, thống kê và các vấn đề liên quan
Năng lực mô hình hóa toán học.
+) Dùng phần mềm Geogebra vẽ biểu đồ từ bảng số liệu thống kê
NĂNG LỰC CHUNG
Năng lực tự chủ và tự học
+) Học sinh chủ động tải phần mềm, sử dụng phần mềm trên cơ sở đã được học ở lớp dưới
+) Học sinh có khả năng thu thập và xử lí số liệu
+) Kết hợp giữa toán học và tin học
+) Chuyển các nội dung toán học vào phần mềm để giải quyết vấn đề. 
Năng lực giao tiếp và hợp tác
+) Học sinh trình bày, thực hành được ba bài toán sau: biểu diễn miền nghiệm của hệ BPT bậc nhất hai aane, vẽ Conic, vẽ biểu đồ, tính toán các số liệu thống kê. 
3. Về phẩm chất:
Trách nhiệm
+) Có ý thức hỗ trợ, hợp tác với các thành viên trong nhóm để hoàn thành nhiệm vụ.
Nhân ái
+) Có ý thức tôn trọng ý kiến của các thành viên trong nhóm khi hợp tác. 
Chăm chỉ
+) Tích cực xây dựng bài, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của GV.
II. Thiết bị dạy học và học liệu: 
Giấy viết, SGK toán 10 tập 1 và tập 2
Máy chiếu, máy tính có cài đặt phần mềm Geogebra để chia lớp thành 4 nhóm thực hành. 
III. Tiến trình dạy học:
Tiết 1, 2 
( gồm hoạt động 1 và hoạt động 2 ) 
Hoạt động 1: Biết biểu diễn miền nghiệm của hệ BPT bậc nhất hai ẩn trên phần mềm 
a) Mục tiêu: 
- Học sinh biết cách sử dụng phần mềm để vẽ miền nghiệm của hệ BPT bậc nhất hai ẩn trên máy tính hoặc điện thoại. 
b) Nội dung:
- GV hướng dẫn HS các bước thực hiện một bài toán: biểu diễn miền nghiệm của hệ BPT bậc nhất hai ẩn
	+) Bước 1. Biểu diễn miền nghiệm của từng BPT trong hệ bằng cách nhật từng BPT vào ô nhập lệnh và bấm enter. 
	+) Bước 2. Miền nghiệm của hệ BPT là giao của các miền giao của từng BPT, tức là phần mặt phẳng được tô đậm hơn. 
Ví dụ 1. Biểu diễn hình học tập nghiệm của hệ BPT bậc nhất hai ẩn sau: 
 (*)
c) Sản phẩm:
 - Miền nghiệm của hệ bất phương trình trên máy tính. ( phần tô đậm hơn) 
Lưu ý: Đường nét liền thể hiện những điểm thuộc miền nghiệm và ngược lại, đườn nét đứt là những điểm không thuộc miền nghiệm. 
d) Tổ chứcthực hiện: PP dạy học theo nhóm, PP đàm thoại – gợi mở, đánh giá bằng phương pháp quan sát, vấn đáp, sản phẩm của nhóm	
Bước 1: Giao nhiệm vụ cho 4 nhóm cùng thực hành: Biểu diễn miền nghiệm của hệ (*) trên phần mềm. 
Bước 2: Các nhóm thực hiện nhiệm vụ, cử đại diện thao tác trên máy tính đã được chuẩn bị sẵn cho từng nhóm
Bước 3: Báo cáo kết quả
Bước 4: Giáo viên hoặc các nhóm khác nhận xét, đánh giá cho các nhóm
Hoạt động 2: Vẽ biểu đồ và tính các số đặc trưng đo xu thế trung tâm, đo mức độ phân tán cho mẫu số liệu không ghép nhóm
a) Mục tiêu: 
- Học sinh biết nhập bảng số liệu thống kê không ghép lớp vào phần mềm. 
- Vẽ biểu đồ thể hiện bảng số liệu thống kê đó
- Dùng phần mềm tính tổng tần số, số trung bình, phương sai, đệ lệch chuẩn, số trung vị, Môt,.. 
b) Nội dung:
Ví dụ 2. Cho bảng số liệu sau: 
Nhiệt độ (đơn vị: 0C) ở Thành phố Hồ Chí Minh ngày 03/6/2021 sau tám lần đo là 
27 26 28 32 34 35 30 28
Vẽ biểu đồ cột mô tả tần số và tìm số trung bình cộng, trung vị, tứ phân vị, phương sai, độ lệch chuẩn của mẫu số liệu trên. 
c) Sản phẩm:
- Các nhóm nhập được số liệu vào máy
- Các nhóm vẽ được biểu đồ: 
- Các nhóm tính được các số liệu như số n, số trung bình cộng, phương sai, độ lệch chuẩn,...
d) Tổ chứcthực hiện: PP dạy học theo nhóm, PP đàm thoại – gợi mở, đánh giá bằng phương pháp quan sát, vấn đáp, sản phẩm của nhóm
Bước 1: Chia lớp thành 4 nhóm
Bước 2: Các nhóm tiến hành thực hành độc lập
Bước 3: Báo cáo kết quả 
Bước 4: Nhận xét, kết luận của GV
Tiết 3
( hoạt động 3, 4) 
Hoạt động 3: Vẽ các đường Cônic
a) Mục tiêu: 
- Học sinh cách xác định (cách vẽ) của từng đường Conic cụ thể trong mặt phẳng. 
- Biết thực hành: Dùng phần mềm GeoGebra để vẽ Conic
b) Nội dung:
b.1) Giới thiệu một số nút công cụ vẽ cơ bản phục vụ cho tiết học
 nút di chuyển đối tượng được chọn
chọn điểm mới 
 vẽ đường thẳng đi qua hai điểm cho trước
 vẽ Elip khi biết hai tiêu điểm và một điểm nằm trên Elip
 Vẽ Hypebol khi biết hai tiêu điểm và một điểm nằm trên Hypebol
vẽ Parabol khi biết tiêu điểm và đường chuẩn
b.2) Hướng dẫn thực hành ba cách vẽ một đường Conic trên phần mềm
- Cách 1. Vẽ Conic dựa vào ba biểu tượng , , 
 ( Việc lấy các tiêu điểm, đường chuẩn có thể lấy tự do hoặc do giáo viên chỉ định ) 
- Cách 2. Vẽ Conic khi tiết tọa độ của các tiêu điểm, một điểm thuộc Conic hoặc biết phương trình đường chuẩn
Cụ thể: 
	+) Vẽ Elip khi biết hai tiêu điểm và một điểm thuộc elip
	 	Nhập lệnh: Elip((-c,0),(c;0),(m,n)) bấm enter
	+) Vẽ Hypebol khi biết hai tiêu điểm và một điểm thuộc elip
	 	Nhập lệnh: Hypebon((-c,0),(c;0),(m,n)) bấm enter
	+) Vẽ Prabol khi biết tiêu điểm và đường chuẩn 
	 	Nhập lệnh: Parabon((c,0),x-a=0) bấm enter
- Cách 3. Vẽ Conic khi biết phương trình chính tắc. 
+) Phương thức 1: Nhập trực tiếp Phương trình chính tắc của Conic vào ô nhập lệnh
Ví dụ:
+) Phương thức 2. Dùng thanh trượt để thay đổi giá trị của tham số, đồng thời quan sát sự thay đổi hình dạng của Conic. 
Bước 1. Tạo thanh trượt ( coi biến trên thanh trượt là tham số ) 
Bước 2. Nhập phương trình của Conic theo tham số 
Ví dụ 1. 
a) Trên mặt phẳng lấy ba điểm phân biệt, cố định và không thẳng hàng 
Vẽ Elip và Hypebol nhận làm hai tiêu điểm và đi qua điểm M
b) Trên mặt phẳng lấy một đường thẳng d và một điểm F không thuộc d cố định. Vẽ Parabol nhận F làm tiêu điểm và d làm đường chuẩn
Ví dụ 2. 
a) Vẽ Elip có hai tiêu điểm là và đi qua điểm 
b) Vẽ Hypebol biết PTCT là 
c) Vẽ Prabol tại các giá trị 
c) Sản phẩm:
Ví dụ 1. 
Ví dụ 2. 
d) Tổ chứcthực hiện: PP dạy học theo nhóm, PP đàm thoại – gợi mở, đánh giá bằng phương pháp quan sát, vấn đáp, sản phẩm của nhóm
Bước 1: Chia lớp thành 4 nhóm 
Bước 2: Các nhóm thực hành độc lập
Bước 3: Báo cáo kết quả
Bước 4: Giáo viên nhận xét, đánh giá
Hoạt động 4: Vẽ đồ thị hàm số bậc hai
a) Mục tiêu: 
- Học sinh sử dụng máy tính bảng, hoặc máy tính xách tay có cài phần mền GeoGebra để vẽ đồ thị hàm số bậc hai. 
- Cài đặt được tham số a,b,c trên phần mền GeoGebra để quan sát sự thay đổi của đồ thị hàm số bậc hai
- Sử dụng kỹ năng về đồ thị hàm số bậc hai trên GeoGebra vào các tình huống thực tế. Thiết kế một cổng Parabol theo kích thước cho trước
b) Nội dung:
Giới thiệu một số nút công cụ vẽ cơ bản phục vụ cho tiết học
 nút di chuyển đối tượng được chọn
chọn điểm mới 
 vẽ đường thẳng đi qua hai điểm cho trước
Cách vẽ đường parabol có phương trình cho trước
c) Sản phẩm
- Các tệp GeoGebra để vẽ đồ thị
- Hình vẽ thiết kế cổng trào Parabol
- Báo cáo quy trình cài đặt và các thao tác trên máy tính xách tay có cài phần mền GeoGebra
d) Tổ chứcthực hiện: PP dạy học theo nhóm, PP đàm thoại – gợi mở, đánh giá bằng phương pháp quan sát, vấn đáp, sản phẩm của nhóm
Bước 1: Chia lớp thành 4 nhóm 
Bước 2: Các nhóm thực hành độc lập
Bước 3: Báo cáo kết quả
Bước 4: Giáo viên nhận xét, đánh giá
HƯỚNG DẪN VỀ NHÀ
1. Tìm một số bài toán có nội dung thực tiễn liên quan đến hàm số bậc nhất, hàm số bậc hai rồi tìm lời giải.
2. Thiết kế một số cổng hình các đường conic ở nơi em sống hoặc học tập.